Number Representations

In conventional notation, numbers can be represented as a combination of a value, or magnitude, a sign, plus or minus, and, if necessary, a decimal point. As a first step in our discussion, let’s consider two different approaches to storing just the value of the number in the computer. The most obvious approach is simply to recognize that there is a direct binary equivalent for any decimal integer.

The range of integers that we can store this way is determined by the number of bits available.Thus, an 8-bit storage location can store any unsigned integer of value between 0 and 255, a 16-bit storage location, 0–65535. If we must expand the range of integers to be handled,we can provide more bits. A common way to do this is to use multiple storage locations. In Figure 5.1, for example, four consecutive 1-byte storage locations are used to provide 32 bits of range. Used together, these four locations can accept 2^32, or 4,294,967,296 different values.

The use of multiple storage locations to store a single binary number may increase thedifficulty of calculation and manipulation of these numbers because the calculation mayhave to be done one part at a time, possibly with carries or borrows between the parts,but the additional difficulty is not unreasonable.Most modern computers provide built-in instructions that perform data calculations 32 bits or 64 bits at a time, storing the data automatically in consecutive bytes. For other number ranges, and for computers without this capability, these calculations can be performed using software procedures within the computer.

An alternative approach known as binary-coded decimal (BCD), may be used in some applications. In this approach, the number is stored as a digit-by-digit binary representation of the original decimal integer. Each decimal digit is individually converted to binary. This requires 4 bits per digit. Thus, an 8-bit storage location could hold two binary-coded decimal digits—in other words, one of one hundred different values from 00 to 99. For example, the decimal value 68 would be represented in BCD as 01101000.

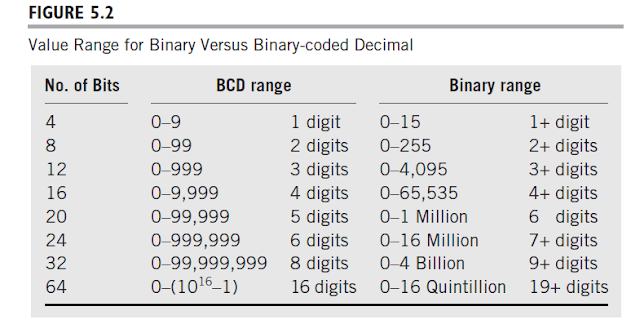
The table in Figure 5.2 compares the decimal range of values that can be stored in binary and BCD forms. Notice that for a given number of bits the range of values that can be held using the binary-coded decimal method is substantially less than the range using conventional binary representation

Signed Integer Representations

With the shortcomings of BCD, it shouldn’t surprise you that integers are nearly always stored as binary numbers. As you have already seen, unsigned integers can be converted directly to binary numbers and processed without any special care. The addition of a sign, however, complicates the problem, because there is no obvious direct way to represent the sign in binary notation. In fact, there are several different ways used to represent negative numbers in binary form, depending on the processing that is to take place. The most common of these is known as 2’s complement representation.Before we discuss 2’s complement representation, we will take a look at two other, simpler methods: sign-and-magnitude representation and 1’s complement representation. Each of these latter methods has some serious limitations for computer use, but understanding these methods and their limitations will clarify the reasoning behind the use of 2’s complementation.

Sign Magnitude Representation

In daily usage, we represent signed integers by a plus or minus sign and a value. This representation is known, not surprisingly, as sign-and-magnitude representation.

In the computer we cannot use a sign, but must restrict ourselves to 0’s and 1’s. We could select a particular bit, however, and assign to it values that we agree will represent the plus and minus signs. For example, we could select the leftmost bit and decide that a 0 in this place represents a plus sign and a 1 represents a minus. This selection is entirely arbitrary, but if used consistently, it is as reasonable as any other selection. In fact, this is the representation usually selected. Figure 5.5 shows examples of this representation.

Suppose 32 bits are available for storage and manipulation of the number. In this case, we will use 1 bit for the sign and 31 bits for the magnitude of the number. By convention, the leftmost, or most significant, bit is usually used as a sign, with 0 corresponding to a plus sign and 1 to a minus sign. The binary range for 32 bits is 0 to 4,294,967,295; we can represent the numbers −2, 147, 483, 647 to +2,147,483,647 this way.

There are several inherent difficulties in performing calculations when using sign-and-magnitude representation. Many of these difficulties arise because the value of the result of an addition depends upon the signs and relative magnitudes of the inputs.In addition to the foregoing difficulty, there are two different binary values for 0,

00000000 and 10000000

representing +0 and −0, respectively. This seems like a minor annoyance, but the system must test at the end of every calculation to assure that there is only a single value for 0. This is necessary to allow program code that compares values or tests a value for 0 to work correctly. Positive 0 is preferred because presenting −0 as an output result would also be confusing to the typical user.

Nine’s Decimal and 1’s Binary Complementary Representations

Nine's Decimal Representation

 Let us begin by considering a different means of representing negative and positive integers in the decimal number system. Suppose that we manipulate the range of a three-digit decimal number system by splitting the three-digit decimal range down the middle at 500. Arbitrarily, we will allow any number between 0and 499 to be considered positive. Positive numbers will simply represent themselves. This will allow the value of positive numbers to be immediately identified. Numbers that begin with 5, 6, 7, 8, or 9 in the most significant digit will be treated as representations of negative numbers. Figure 5.6 shows the shift in range.

One convenient way to assign a value to the negative numbers is to allow each digit to be subtracted from the largest numeral in the radix. Thus, there is no carry, and each digit can be converted independently of all others. Subtracting a value from some standard basis value is known as taking the complement of the number. Taking the complement of a number is almost like using the basis value as a mirror. In the case of base 10 radix, the largest numeral is 9; thus, this method is called 9’s complementary representation.

Adding two numbers in 9's complement Arithmetic

Add the two numbers. If the result flows into the digit beyond the specified number of digits, add the carry into the result. This is known as end-around carry. Figure 5.10 illustrates the procedure. Notice that the result is now correct for both examples.

Although we could design a similar algorithm for subtraction, there is no practical reason to do so. Instead, subtraction is performed by taking the complement of the subtrahend (the item being subtracted) and adding to the minuend (the item being subtracted from). In this way, the computer can use a singleaddition algorithm for all cases.

It is just as easy to detect overflow in a 9’s complement system, even though the use of modular arithmetic assures that an extra digit will never occur. In complementary arithmetic, numbers that are out of range represent the opposite sign. Thus, if we add

300 + 300 = 600 (i.e.,−399)

both inputs represent positive numbers, but the result is negative. Then the test for overflow is this: If both inputs to an addition have the same sign, and the output sign is different, overflow has occurred.

Steps to Find 9's Complement:

1. Write the given number.
2. Subtract each digit of the number from 9.

Example:

Let's calculate the 9's complement of the number 4567.

1. Write the number:
   4567

2. Subtract each digit from 9:

   • 9 - 4 = 5
   • 9 - 5 = 4
   • 9 - 6 = 3
   • 9 - 7 = 2

3. Resulting 9's complement: 5432

Verification:

If we add the number and its 9's complement, the sum should be $10^n - 1$, where $n$ is the number of digits.
For $4567 + 5432$:

$$4567 + 5432 = 9999$$

This confirms the 9's complement calculation is correct.

Steps for Subtraction Using 9's Complement:

To compute $A-B$ using 9's complement:

1. Find the 9's complement of $B$: Subtract each digit of $B$ from 9.

2. Add $A$ and the 9's complement of $B$: Perform regular addition.

3. Adjust the result:

   • If there's a carry, add 1 to the result and discard the carry.
   • If there's no carry, take the 9's complement of the result to get the negative value.

---

Example: $4567-1234$

Step 1: Find the 9's complement of $B$ (1234):

• $9-1=8$
  
• $9-2=7$
  
• $9-3=6$
  
• $9-4=5$
  

The 9's complement of $\mathrm{1234 }$is 8765.

---

Step 2: Add $A$ (4567) and 9's complement of $B$ (8765):

$$4567+8765=13332$$

Step 3: Adjust the result:

• Since there is a carry (1), add it to the least significant digit: $$3332+1=3333$$
  

Thus, the result of $4567-1234$ is 3333.

---

Key Points:

• Carry occurs: Add 1 to the result and discard the carry.
• No carry: Take the 9's complement of the result to represent the negative value

ONE’S COMPLEMENT The computer can use the binary version of the same method of representation that we have just discussed.the 1’s complement of a number is performed simply by changing every 0 to a 1 and every 1 to a 0.

Addition also works in the same way. To add two numbers, regardless of the implied sign of either input, the computer simply adds the numbers as though they were unsigned integers. If there is a carryover into the next bit beyond the leftmost specified bit, 1 is added to the result, following the usual end-around carry rule. Subtraction is done by inverting the subtrahend (i.e., changing every 0 to 1 and every 1 to 0) and adding. Overflows are detected in the same way as previously discussed: if both inputs are of the same sign, and the sign of the result is different, overflow has occurred; the result is outside the range.Notice that this test can be performed simply by looking at the leftmost bit of the two inputs and the result.

1’s Complement Addition/Subtraction

Steps for 1’s Complement Addition:

1. Add the two binary numbers.

2. If there's a carry-out, add it back to the result (this is called end-around carry).

3. If no carry, the result is the answer.

4. If the sum represents a negative number, take its 1's complement to get the magnitude.

Example 1: Add +5 and -3 using 1’s complement (in 4 bits)

Step 1: Represent in binary (4 bits):

• +5 = 0101

• -3:

  • +3 = 0011

  • 1’s complement = 1100 → this is -3

Step 2: Add

  0101   (+5)
+ 1100   (-3)
-------
 10001

Step 3: Handle the carry (end-around carry):

• Carry out = 1 → Add it back to the LSB:

0001 + 1 = 0010

Final Result: 0010 = +2

Example 2: Add -4 and -3 (in 4 bits)

Step 1: Represent in binary:

• +4 = 0100 → 1’s complement = 1011 = -4

• +3 = 0011 → 1’s complement = 1100 = -3

Step 2: Add

  1011  (-4)
+ 1100  (-3)
-------
 10111

Step 3: Handle carry (add end-around carry):

• Carry = 1

• Result = 0111 + 1 = 1000

Now the result is in 1’s complement and negative

• So it is -0111 → take 1’s complement to find magnitude:

  • 1000 → 1’s complement = 0111 = 7

Final Answer: -7

Example 3: Subtract 3 - 5 (in 4 bits)

Step 1: Represent in binary:

• 3 = 0011

• 5 = 0101 → 1’s complement = 1010 (represents -5)

Step 2: Add

  0011
+ 1010
-------
 1101

No carry → Negative result

• So answer is in 1’s complement: 1101

• Take 1’s complement → 0010 = 2

Final Answer: -2

Ten's Compliment and Two's Compliment

Ten's Complement

You have seen that complementary representation can be effective for the representation and calculation of signed integer numbers. As you are also aware, the system that we have described,which uses the largest number in the base as its complementary reflection point, suffers from some disadvantages that result from the dual zero on its scale. 

By shifting the negative scale to the right by one, we can create a complementary system that has only a single zero. This is done by using the radix as a basis for the complementary operation. In decimal base, this is known as the 10’s complement representation. The use of this representation will simplify calculations. The trade-off in using 10’s complement representation is that it is slightly more difficult to find the complement of a number. A three-digit decimal scale is shown in Figure 5.12.

The theory and fundamental technique for 10’s complement is the same as that for 9’s complement. The 10’s complement representation uses the modulus as its reflection point.The modulus for a three-digit decimal representation is 1000, which is one larger than the largest number in the system, 999.

                                10's comp = 9's comp + 1

To add two numbers in 10’s complement, one simply adds the digits; any carry beyond the specified number of digits is thrown away. Subtraction is again performed by inverting the subtrahend and adding.

Two's Complement

Two’s complement representation for binary is, of course, similar to 10’s complement representation for decimal. In binary form, the modulus consists of a base 2 ‘‘1’’ followed by the specified number of 0s. For 16 bits, for example, the modulus is 10000000000000000

As was true for the 10’s complement, the 2’s complement of a number can be found in one of two ways: either subtract the value from the modulus or find the 1’s complement by inverting every 1 and 0 and adding 1 to the result.

Figure 5.13 shows an 8-bit scale for 2’s complement representation.

Two’s complement addition, like 10’s complement addition in decimal, consists of adding the two numbers mod<themodulus>. This is particularly simple for the computer, since it simply means eliminating any 1s that don’t fit into the number of bits in the word. Subtraction and overflow are handled as we have already discussed.

As in 10’s complement, the range is unevenly divided between positive and negative.

The range for 16 bits, for example, is −32768 ≤ value ≤32767.

The use of 2’s complement ismore common in computers than is 1’s complement, but both methods are in use. The trade-off is made by the designers of a particular computer: 1’s complement makes it easier to change the sign of a number, but addition requires an extra end-around carry step. One’s complement has the additional drawback that the algorithm must test for and convert−0 to 0 at the end of each operation. Two’s complement simplifies the addition operation at the expense of an additional add operation any time the sign change operation is required.

This example shows each of the four possible outcomes that can result from the addition of two 4-bit 2’s complement numbers.

Example 1: Add +5 and -3 (4 bits)

Step 1: Represent in binary (4-bit signed):

• +5 = 0101

• -3:

  • +3 = 0011

  • 1’s complement = 1100, add 1 → 1101

Step 2: Add

  0101
+ 1101
-------
 10010

Step 3: Handle overflow
We only keep the lower 4 bits, discard overflow bit
Result = 0010 = +2

Example 2: Add -4 and -3 (4 bits)

Step 1: Represent in 2’s complement:

• +4 = 0100 → 2’s complement = 1100

• +3 = 0011 → 2’s complement = 1101

Step 2: Add

  1100
+ 1101
-------
 11001

Ignore the carry-out (5th bit). Keep only 4 bits:
Result = 1001

• This is negative → take 2’s complement to find magnitude:

  • Invert 1001 → 0110, add 1 → 0111 = 7

Final Answer: -7

Example 3: Subtract 5 - 3 (4 bits)

Step 1: Represent:

• +5 = 0101

• -3 = 2’s complement of 0011 = 1101

Step 2: Add

  0101
+ 1101
-------
 10010

Ignore overflow → Result = 0010 = +2

Example 4: Subtract 3 - 5 (4 bits)

Step 1: Represent:

• +3 = 0011

• -5 = 2’s complement of 0101 = 1011

Step 2: Add

  0011
+ 1011
-------
 1110

Result = 1110
→ Negative → Take 2’s complement to find magnitude:

• Invert: 0001, Add 1 = 0010 = 2

Final Answer: -2

Summary of Rules for Complementary Numbers

The following points summarize the rules for the representation and manipulation of complementary numbers, both radix and diminished radix, in any even number base. For most purposes you will be interested only in 2’s complement and 16’s complement:

1. Remember that the word ‘‘complement’’ is used in two different ways. To complement a number, or take the complement of a number, means to change its sign. To find the complementary representation of a number means to translate or identify the representation of the number just as it is given.

2. Positive numbers are represented the same in complementary form as they would be in sign and magnitude form. These numbers will start with 0, 1, . . . N/2–1. For binary numbers, positive numbers start with 0, negative with 1.

3. To go from negative sign-and-magnitude to complementary form, or to change the sign of a number, simply subtract each number from the largest number in the base (diminished radix) or from the value 100 . . . , where each zero corresponds to a number position (radix). Remember that implied zeros must be included in the procedure. Alternatively, the radix form may be calculated by adding 1 to the diminished radix form. For 2’s complement, it is usually easiest to invert every digit and add 1 to the result.

4. To get the sign-and-magnitude representation for negative numbers, use the procedure in (2) to get the magnitude. The sign will, of course, be negative. Remember that the word size is fixed; there may be one or more implied 0s at the beginning of a number that mean the number is really positive.

5. To add two numbers, regardless of sign, simply add in the usual way. Carries beyond the leftmost digit are ignored in radix form, added to the result in diminished radix form. To subtract, take the complement of the subtrahend and add.

6. If we add two complementary numbers of the same sign and the result is of opposite sign, the result is incorrect. Overflow has occurred.